文章导读

手性诱导自旋选择性（CISS）效应表明，电子在通过手性分子传输时会发生自旋过滤，这一现象在自旋电子学和对映选择性化学中具有重要应用前景。然而，其物理机制仍存在争议，特别是关于衬底自旋轨道耦合（SOC）的作用。本文作者通过研究吸附在 \( \text{Cu}(332) \)、\( \text{Ag}(110) \) 和 \( \text{Au}(111) \) 表面上的纯对映体七螺旋烯（\( [7]\text{H} \)）单层，探讨了低能光电子与有序手性分子单层的相互作用。

实验利用紫外激光脉冲激发金属衬底产生光电子，并通过 Mott 极化计测量透射电子的纵向自旋极化。结果显示，\( [7]\text{H} \) 分子单层能产生约 \( 6\% \) 至 \( 8\% \) 的纵向自旋极化（\( P_Z \)），且极化方向严格依赖于分子的螺旋手性（\( M \)-型或 \( P \)-型）。结合自旋分辨密度泛函理论（DFT）计算和模型哈密顿量分析，研究结果支持了在分子静电势诱导的自旋轨道耦合作用下，电子沿螺旋路径传输的半经典图像。

Table of Contents

💡 核心创新点

  • 明确的手性-自旋耦合关系： 实验证实，电子穿过 \( [7]\text{H} \) 单层后的自旋极化方向取决于分子的手性，\( (M) \)-型和 \( (P) \)-型对映体分别导致相反符号的净自旋极化。
  • 广谱适用性与机制验证： 在不同 SOC 强度的衬底（Cu, Ag, Au）上均观察到类似的自旋过滤效应，表明该效应主要源于手性分子本身而非衬底诱导的 SOC。
  • 全碳芳香体系的 CISS 效应： 首次在仅由碳和氢组成的高导电性芳香族螺旋分子单层中观测到显著的 CISS 效应，扩展了该效应的材料体系。
  • 理论模型的定性一致性： 结合 DFT 和紧束缚模型计算，定性复现了实验观测到的自旋极化符号与分子螺旋性的关系，支持了螺旋电场诱导 SOC 的物理机制。

🔬 图文深度解析

图 1：分子结构与实验装置

[7]H 对映体的球棍模型及实验装置示意图
Figure 1：(a) \( [7]\text{H} \) 两种对映体的球棍模型，\( (M) \)-\( [7]\text{H} \) 为左手螺旋，\( (P) \)-\( [7]\text{H} \) 为右手螺旋；(b) 单个 \( (M) \)-\( [7]\text{H} \) 分子在金属表面的取向示意图；(c) \( (M) \)-\( [7]\text{H} \) 在 \( \text{Cu}(111) \) 上观测到的单层结构示意图；(d) 包含 Mott 分析器的光电子发射实验装置示意图。

作者首先展示了研究对象七螺旋烯（\( [7]\text{H} \)）的分子结构。如图 1a 所示，该分子由7个苯环角向稠合而成，由于空间位阻效应形成螺旋结构，存在 \( (M) \) 和 \( (P) \) 两种镜像异构体。图 1b 和 1c 展示了分子在金属表面的吸附模式，其下层苯环平行于表面，其余部分向上螺旋延伸，并在表面形成有序单层。图 1d 描述了实验原理：利用 \( \lambda = 213 \ \text{nm} \) 的紫外激光激发金属衬底产生光电子，电子穿过分子层后进入 Mott 极化计进行自旋分析。该装置能够通过改变入射光的偏振状态（线偏振或圆偏振）来调控初始激发电子的自旋状态。

这一部分的结构表征为后续理解电子传输路径奠定了基础，特别是分子在表面的直立螺旋取向是实现定向自旋过滤的关键几何条件。

图 2：自旋极化测量结果

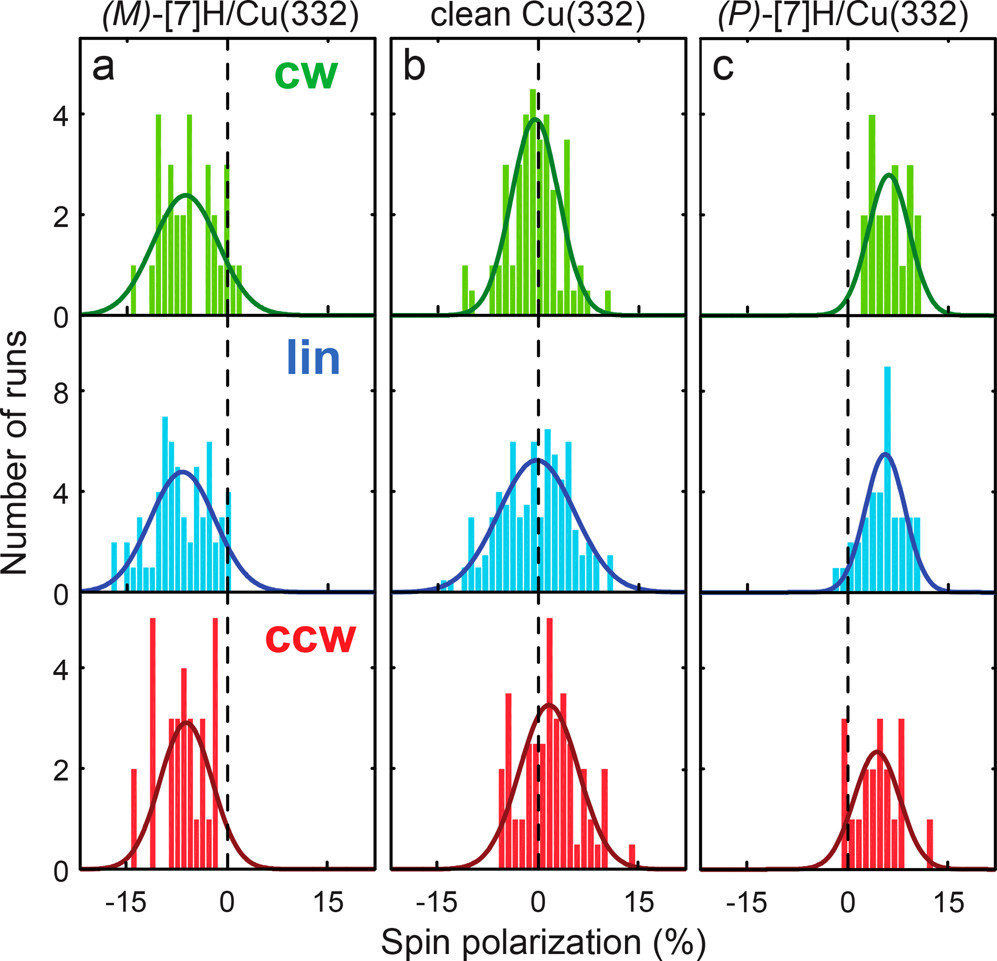
电子自旋极化直方图
Figure 2：来自 (a) \( (M) \)-\( [7]\text{H} \)，(b) 清洁 \( \text{Cu}(332) \)，和 (c) \( (P) \)-\( [7]\text{H} \) / \( \text{Cu}(332) \) 表面的电子自旋极化 \( P_Z \)。上行（绿色）和下行（红色）分别表示使用顺时针（cw）和逆时针（ccw）圆偏振紫外光激发的实验，中间行（蓝色）表示线偏振光激发。注意 (b) 列纵坐标数值相对于 (a) 和 (c) 缩小了 2 倍。

图 2 是本文的核心实验结果。中间列显示清洁铜表面的自旋极化几乎为零，符合非磁性金属的预期。对比左右两列可以看出显著的自旋过滤效应：当电子穿过 \( (M) \)-\( [7]\text{H} \) 单层时（左列），无论入射光偏振如何，出射电子均表现出约 \( -6\% \) 的净自旋极化（倾向于自旋向下）；而穿过 \( (P) \)-\( [7]\text{H} \) 单层时（右列），则表现出约 \( +5.5\% \) 至 \( +6.1\% \) 的正自旋极化（倾向于自旋向上）。这一结果直接证明了透射电子的优先自旋方向取决于吸附分子的螺旋手性，且该效应在 \( \text{Cu}(332) \) 表面上具有高度的可重复性和对映选择性。

该数据有力地支持了 CISS 效应，表明即使在单分子层尺度，有机手性分子也能作为有效的电子自旋过滤器。

图 3：电子结构计算

[7]H 的吸附构型、结合能及态密度
Figure 3：(a) \( [7]\text{H} \) 沉积在 \( \text{Cu}(332) \)、\( \text{Ag}(110) \) 和 \( \text{Au}(111) \) 上的吸附构型及结合能；(b) 投影电子态密度（PDOS）及分子轨道能级位置；(c) \( [7]\text{H} \) 选定电子态（HOMO, LUMO, LUMO+9）的轨道电荷密度分布。

为了探究电子传输的微观机制，作者进行了 DFT 计算。图 3a 显示 \( [7]\text{H} \) 在 \( \text{Cu}(332) \) 上结合最强（\( E_{BE} = -2.22 \ \text{eV} \)），而在 Ag 和 Au 上较弱。图 3b 的态密度分析表明，分子轨道与金属衬底发生杂化。重要的是，图 3c 展示了分子轨道的空间分布，HOMO 和 LUMO 等轨道沿着分子的螺旋骨架分布，这意味着电子在传输过程中被迫沿螺旋路径运动。这种几何约束使得电子感受到由分子静电势引起的有效螺旋电场，从而产生自旋轨道耦合作用。

这些计算结果为“电子沿螺旋路径传输”的半经典图像提供了量子力学基础，解释了为何全碳骨架也能产生显著的 SOC 效应。

图 4：模型哈密顿量模拟

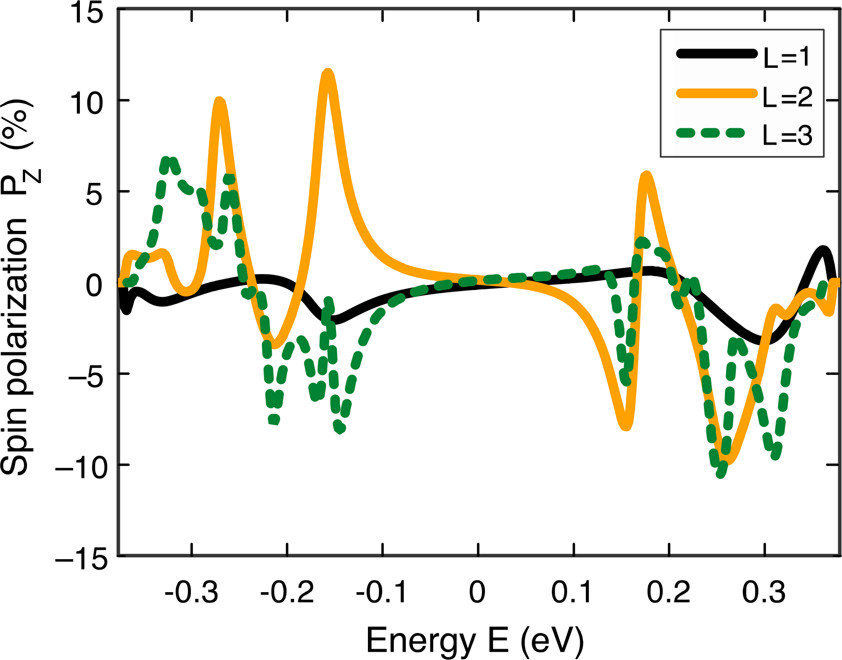
模型螺旋系统的自旋极化模拟结果
Figure 4：针对不同数量的左手螺旋匝数 \( L \)，计算得到的模型螺旋系统的自旋极化随能量和长度的依赖关系。强烈的能量依赖性反映了紧束缚模型电子谱的离散结构。

作者利用唯象模型哈密顿量计算了电子通过螺旋势场后的自旋极化率。图 4 显示，自旋极化的大小和符号强烈依赖于电子能量，但在特定能量窗口下可达到 \( |P_Z| \approx 10\%-15\% \)，这与实验观测的数量级（\( 6\%-8\% \)）吻合。模拟还表明，增加螺旋匝数（\( L \)）通常会增强自旋极化效应。重要的是，该模型定性地重现了自旋极化符号随螺旋手性翻转的现象。

这一理论工作进一步确认了螺旋电场导致的 SOC 是 CISS 效应的主要物理来源。

⚗️ 总结与展望

本文作者通过光电子能谱实验，系统研究了 \( [7]\text{H} \) 分子单层在不同金属基底上的电子自旋过滤行为。实验数据表明，电子的纵向自旋极化具有强烈的手性依赖性：\( (M) \)-对映体倾向于传输自旋向下的电子，而 \( (P) \)-对映体倾向于传输自旋向上的电子。值得注意的是，这种效应在自旋轨道耦合强度差异巨大的 Cu、Ag 和 Au 衬底上均被观测到，且由分子手性引起的净自旋极化差异（\( \Delta P_Z \)）在三种衬底上保持一致（约 \( 11\%-16\% \)），有力地证明了手性分子本身是产生自旋过滤的主导因素，排除了衬底诱导机制的主导地位。结合 DFT 和紧束缚模型计算，作者提出电子在分子螺旋轨道中的传输受到由分子静电势产生的螺旋电场影响，进而通过自旋轨道耦合实现自旋选择性。该研究不仅拓展了 CISS 效应的材料体系至全碳芳香分子，也为其物理机制提供了关键的实验证据和理论支持。